[1790 vues] 2021-11-18 Emmanuel Orchanian
Introduction
Le modulo est une opération mathématique comme l'addition, la soustraction, la multiplication et la division.
On le note "mod" ou par le signe pourcentage %,
Par exemple 5 % 2 = 1 se lit "cinq modulo deux est égal à un"
Note : même si on utilise le signe pourcent, ça n'a aucun rapport avec les pourcentages ! (comme c'est souvent le cas en informatique, les signes qu'on utilise n'ont aucun rapport avec leur signification normale...)
On connait le modulo depuis l'école primaire !
À l'école primaire, nous faisions les divisions de la sorte :

On lisait ainsi : "cinq divisé par deux donne deux, et il reste un"
Le modulo, c'est le reste de la division
Programmation
- En JavaScript et PHP, on utilise le signe pourcent :
5 % 2 - Pour les recherches Google (pour information on peux faire des calculs si on les tape dans Google), il faut écrire "mod", par exemple cherchez sur Google
5 mod 2(je viens de voir que le signe % fonctionnait aussi !)
Attention danger
Sur cette page on ne traite pas du cas des nombres plus petits que zéro, les négatifs.
Utilisation pratique en programmation
Vous voulez afficher en boucle "lundi, mardi, mercredi etc."
jours_de_la_semaine =
[
0 : "Lundi",
1 : "Mardi",
2 : "Mercredi" ,
3 : "Jeudi",
4 : "Vendredi",
5 : "Samedi",
6 : "Dimanche"
]
Pour i de 0 à 200 {
écrire jours_de_la_semaine[i % 7]
}
Ainsi, le [i % 7] vaudra 0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3...
Tandis que le i vaut 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14...
(Petit parenthèse de programmeur : chez les américains les jours commencent par dimanche et non lundi, ainsi le 0 sera dimanche, le 1 lundi, le 2 mardi, ..., et le 6 samedi.)
Quelque modulos dans la vraie vie
- Les secondes et les minutes : modulo 60
- Les heures françaises : modulo 24
- Les heures américaines : modulo 12
- Les jours de la semaine : modulo 7
- Les degrés pour un cercle : modulo 360
En connaissez-vous d'autres ?
(Et pour celles et ceux qui veulent aller plus loin...)
Quelque exemples
- 10 % 7 = 3 Quand on divise 10 par 7, il reste 3 (dix modulo sept vaut trois)
- 10 % 10 = 0 Quand on divise 10 par 10, il reste 0 (dix modulo dix vaut zéro)
- 10 % 3 = 1 Quand on divise 10 par 3, il reste 1 (dix modulo trois vaut 1)
- 3 % 2 = 1 Quand on divise 3 par 2, il reste 1 (trois modulo deux vaut un)
- 3 % 15 = 3 Quand on divise 3 par 15, il reste 3 (trois modulo quinze vaut trois)
- 10157 % 7986 = 2171 Quand on divise 10157 par 7986, il reste 2171 (pas envie d'écrire)
Étude de cas de la table de modulo 3
0 % 3 = 0
1 % 3 = 1
2 % 3 = 2
3 % 3 = 0
4 % 3 = 1
5 % 3 = 2
6 % 3 = 0
7 % 3 = 1
8 % 3 = 2
9 % 3 = 0
10 % 3 = 1
11 % 3 = 2
12 % 3 = 0
13 % 3 = 1
14 % 3 = 2
15 % 3 = 0
16 % 3 = 1
17 % 3 = 2
18 % 3 = 0
19 % 3 = 1
20 % 3 = 2
21 % 3 = 0
22 % 3 = 1
Que remarquez-vous ? (indice : observez les résultats)
Les résultats font en boucle 0 1 2 , 0 1 2 , 0 1 2 ...

Règles générales
Pour modulo "X"
- Le modulo de X ne sera jamais égal à X (par exemple avec modulo 3, on a 0, 1, 2 mais pas 3)
- Plus généralement, le modulo de X ne sera jamais plus grand que X
- On a constamment des boucles qui commencent à zéro et finissent à "X-1"
- La longueur de chaque boucle est de X (par exemple, pour modulo 3, la boucle est composée de 3 éléments, 0, 1 et 2)
- La boucle avance 1 par 1
- Si on augmente le maximum de la boucle de 1, on a le modulo utilisé
Quelques boucles pour exemple
- Pour 3 :
0 1 2 0 1 2 0 1 2... - Pour 5 :
0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4... - Pour 12 :
0 1 2 3 4 5 6 7 8 9 10 11 0 1 2 3 4 5 6 7 8 9 10 11 0 1... - Pour 2 :
0 1 0 1 0 1 0 1 0 1 0 1 0 1... - Pour 1 :
0 0 0 0 0 0 0 0... (quand on divise par 1, il n'y a jamais de reste) - Pour 4 :
0 1 2 3 0 1 2 3 0 1 2 3 0 1 2...
Graphique du modulo
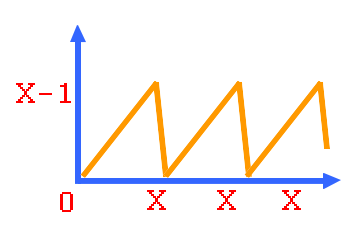
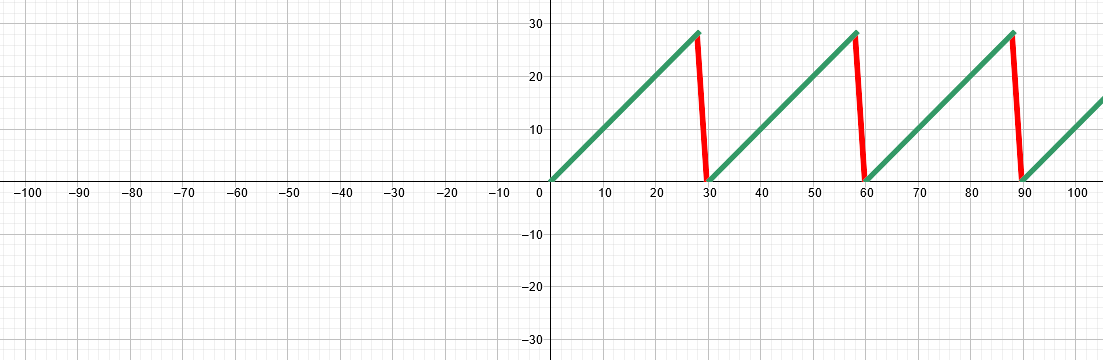
(X%30)
Éthymologie
Le mot modulo vient du latin modulus qui signifie "mesure".
Autres articles qui pourraient vous intéresser
- ➕➖➗Opérations mathématiques de base en codage
- 🔁 Modulo : vous le connaissez depuis l'école primaire !
Merci d'avoir lu !
Si en général vous avez une question, une curiosité, n'hésitez pas me contacter.